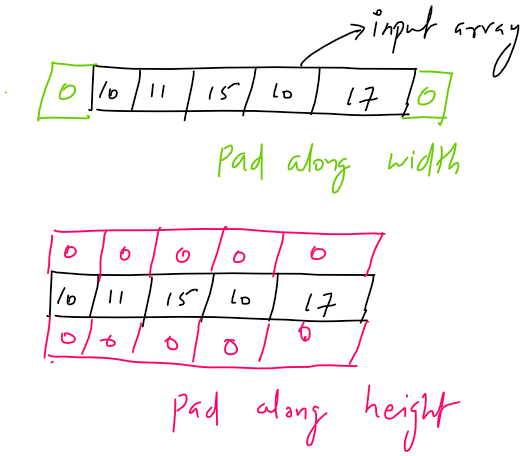
Padding means expanding the input array with value (called pad value). The pad values (commonly zero) can be added along the height or width of the input array.

pad along width and height

The output shape of a convolution operation is defined as follows,

\[output = \lfloor {\frac {(input - kernel + 2 * padding)} {stride}} \rfloor + 1\]

The Convolution layer in TensorFlow has two types of padding- VALID and SAME.

VALID padding

In VALID padding no pad value is added to the input. Hence, the shape of the array is preserved. Below is the equation for the output shape.

\[output\_height = \lfloor {\frac {(input\_height - kernel\_height)} {stride\_along\_height}} \rfloor + 1\] \[output\_width = \lfloor {\frac {(input\_width - kernel\_width)} {stride\_along\_width}} \rfloor + 1\]

SAME padding

In SAME padding we have to pad such a way that,

\[output\_height = \lceil {\frac {input\_height} {stride\_along\_height}} \rceil\] \[output\_width = \lceil {\frac {input\_width} {stride\_along\_width}} \rceil\]

To satisfy the above constraints, the input array has to be modified. From deriving the number of padding needed from the first equation, we get,

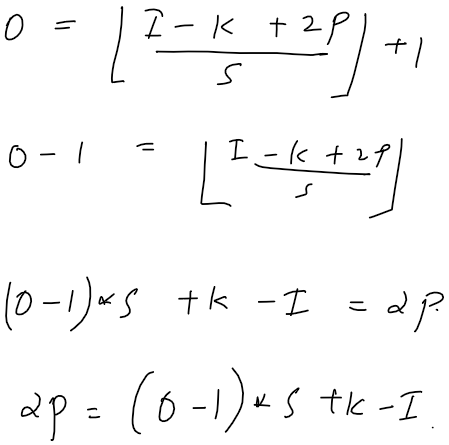
Derivation

\[number\_of\_padding\_along\_height = (output\_height - 1) * stride\_along\_height - input\_height + kernel\_height\] \[number\_of\_padding\_along\_width = (output\_width - 1) * stride\_along\_width - input\_width + kernel\_width\]

Now that we have the number of padding along the height, we have to decide the number of paddings that has to be applied on the top and bottom of the input array. In TensorFlow, the padding for the top and bottom is calculated as follows,

\[top\_padding = \lfloor \frac{number\_of\_padding\_along\_height}{2} \rfloor\] \[bottom\_padding = number\_of\_padding\_along\_height - top\_padding\]

The above equations imply that bottom_padding has higher priority than top_padding.

Similarly, for deciding padding for left and right,

\[left\_padding = \lfloor \frac{number\_of\_padding\_along\_width}{2} \rfloor\] \[right\_padding = number\_of\_padding\_along\_width - left\_padding\]

The above equations imply that right_padding has higher priority than left_padding. It means that when the number of pad along width is one, then we should pad right.

Let’s look at the code.

def calculate_padding_for_same_pad(input_sz, kernel_sz, stride):
    output_sz = np.ceil(input_sz / stride)
    total_pad = (output_sz - 1) * stride - input_sz + kernel_sz
    low_priority_pad = total_pad // 2
    high_priority_pad = total_pad - low_priority_pad
    return low_priority_pad, high_priority_pad
pad_top, pad_bottom = calculate_padding_for_same_pad(input_sz_h, kernel_sz_h, stride_h)
pad_left, pad_right = calculate_padding_for_same_pad(input_sz_w, kernel_sz_w, stride_w)

Reference: